\( \epsilon = 0 \) の場合
この場合は厳密に解けるので、特別扱いします。頂点数毎の非同型なグラフの個数は OEIS で調べられます(リンク)。これによると、頂点数4では11個、頂点数5では34個、頂点数6では156個のグラフが存在します。よって、必要なグラフの個数 M に合わせて、頂点数 N を選んで、非同型なグラフを M 個構築すれば良いでしょう。非同型なグラフを列挙したり、クエリに答える際に、グラフの同型判定が必要になりますが、同型なグラフの「標準系」を定義するのが簡便でしょう。グラフの文字列表現は問題文で定義されていますが、文字列表現が辞書順最小になるような頂点の番号付けを標準系とすれば良いです。
解法1: 次数列で分類する
まず、グラフの次数列(各頂点の次数を降順に並べたもの)に注目する解法を考えましょう。これは最終的な解法ではありませんが、部品として利用します。
基本的な考え方は、グラフの次数列が \( (d_1, d_2, \ldots , d_N) \) であるならば、ノイズを与えたあとのグラフの次数列の期待値は \( ( (1 - \epsilon) d_1 + \epsilon (N - 1 - d_1), \ldots, (1 - \epsilon) d_N + \epsilon (N - 1 - d_N) ) \) になるだろうということです。
注:この考え方は実は正しくありません。yunix さんのこちらのツイートを参照ください。ただ、ある程度の近似にはなるので、この記事では「ある程度の近似になっている」として進めます。
とりあえず、できるだけ多様な次数列を持つグラフを M 個構築したとして(方法は後述します)、クエリの答え方を考えます。
構築したグラフそれぞれについて、ノイズを与えたあとのグラフの次数列の期待値を求めておきます。そして、与えらえたグラフの次数列を計算し、ノイズを与えた後の次数列の期待値がそれに最も「近い」グラフを返せば良いです。「近い」の定義ですが、次数を降順にソートした後の次数列をベクトルと見てユークリッド距離を計算すれば良いでしょう。
この方法がうまくいくためには、できるだけ距離が離れている次数列を持つようなグラフを構築する必要があります。私は次のような方法でグラフを構築しました。
- ランダムなグラフを大量に準備する。
- まず、空グラフと完全グラフを選択するグラフの集合 S に追加する。
- 次の操作を S のサイズが M になるまで繰り返す : 準備したランダムなグラフのうち、S に追加されているグラフの次数列との距離の最小値が最大になるようなグラフを S に追加する。
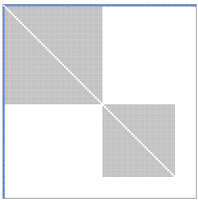
ランダムなグラフの準備の仕方ですが、単純にランダムに辺を選択すると、なだらかな次数列を持つグラフばかりができてしまうので、偏りがある次数列を持つようなグラフをたくさん作ることが必要です。そのためには、様々な大きさのクリークや独立集合を組み合わせたグラフを作ると良いでしょう。行列表示だと以下のようなグラフです。
解法2: 辺の有無の差が最小になるようなグラフを選択する
解法1ではグラフの情報を次数列しか使っていません。次数列が同じグラフはたくさんあるので、これは多くの情報を使っていないことになります。
そこで、与えられたグラフに対して、辺の有無の差が最小になるようなグラフを選択することを考えます。
辺の有無の差を計算するには、ターゲットとなるグラフを固定した上で、頂点の対応付けを求める必要があります。これを簡単にするために、構築するグラフは次のような 3x3 のブロック行列に対応するようなグラフに限定することにします。
そうすると、頂点の対応付けは、各頂点がどのブロックに対応しているかだけを決めれば良いことになります。そのために、次のような山登りアルゴリズムを実装しました。
- まず、頂点を次数順にソートして、ターゲットとなるグラフの次数順にソートしたブロックに対応させる
- 違うブロックに対応している任意の二頂点を選んで、入れ替えたときに一致する辺が増えるかどうかを判定し、増えるならば入れ替える。これを繰り返す。
このアルゴリズムを M 個のグラフに対して実行して、辺の有無の差が最小になるようなグラフを選んで出力すれば良いのですが、そうすると山登りに十分な時間を使うことができず、うまくいきません。
そこで、解法1を利用して、次数列だけに注目して候補を10個に絞ってから、上述の山登りアルゴリズムを実行して、辺の有無の差が最小になるグラフを選ぶという方法を実装しました。
このように、精度が低いが高速な方法で候補を絞ってから、精度が高い方法でランク付けをする手法は、実際の検索システムや推薦システムでよく使われている手法で、一般的に有効な考え方と言えるでしょう。
次に、M 個のグラフを構築する方法を考えます。解法1と同じように、集合から一番「遠い」グラフを逐次追加していく貪欲法を行いますが、今度は距離の定義を「辺の有無の差の数」で定義することにします。
ここで上述山登りアルゴリズムを使うと時間がかかりすぎてうまくいきません。そこで、ブロックグラフ同士のみを比較することに注目して、ブロックの並べる順序を \( 3! \times 3! \) 通り試して、辺の有無の差の数が最小値を計算しました(両方のグラフのブロック順序を反転しても変わらないことに注目すると半分にできます)。
その他の工夫
頂点のマッチングが成功しやすいグラフの作り方
上述の山登りアルゴリズムが成功するためには、次数順に頂点を対応させる初期状態がそれなりに良い必要があります。そのため、ブロック毎の次数の差が小さいグラフは採用しないようにしました。具体的には、少なくとも次数の差が N / 10 以上あるグラフのみを採用することにしました。
空グラフ・完全グラフとの混同が起きやすい問題
公式解説でも言及されていますが、空グラフにノイズを与えたグラフに、一部密度が高い部分ができてしまって、他のグラフと混同しやすいという現象があります。完全グラフについても同様です。
この問題に対処するために、構築するグラフ間の距離を計算する際に、片方が空グラフまたは完全グラフになる場合には、距離を0.5倍扱いするというハックを入れました。非常にアドホックなハックですが、スコアには有効で、コンテスト終了2日前に7位から1位に浮上することができました。
3x3 ブロック行列以外のパターン
\( \epsilon \) が小さい場合は 4x4 ブロック行列が有効な場合があったので、採用しました。また、\( \epsilon \) が大きい場合は 2x2 ブロック行列のみを使った方がスコアが高くなったので、そのようにしました。\( \epsilon \) が大きい場合はブロックが3個あると頂点のマッチングに失敗する確率が上がりすぎてしまったからだと思われます。
当たりの乱数ガチャを固定
各 \( M, \epsilon \) に対して最もスコアの期待値が高くなる N は事前計算で求めておいて固定します。これに加えて、スコアの期待値が高くなる乱数も固定します。上述のアルゴリズムでも、距離が同じグラフが複数ある場合にどのグラフを選ぶかで最終的に選ばれる M 個のグラフは変わってきます。そこで、乱数の seed に対して決定的に動作するようにアルゴリズムを実装した上で、各 \( M, \epsilon \) に対して最もスコアの期待値が高くなる seed を事前計算しました。これは細かい改善ですが計算リソースを必要とするため、最後の一押しとして実行しました。



.gif)


0 件のコメント:
コメントを投稿